Potential game

A game in game theory is considered a potential game if the incentive of all players to change their strategy can be expressed in one global function, the potential function. The concept was proposed by Dov Monderer and Lloyd Shapley. Games can be either ordinal or cardinal potential games. In cardinal games, the difference in individual payoffs for each player from individually changing one's strategy ceteris paribus has to have the same value as the difference in values for the potential function. In ordinal games, only the signs of the differences have to be the same.

The potential function is a useful tool to analyze equilibrium properties of games, since the incentives of all players are mapped into one function, and the set of pure Nash equilibria can be found by locating the local optima of the potential function.

Contents

Definition

Formally, let N be the number of players, A the set of action profiles over the action sets 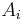A_{i} of each player and u the payoff function. Then, a game 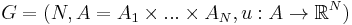G=(N,A=A_{1}\times...\times A_{N}, u: A \rightarrow \reals^N) is a (cardinal) potential game if there is an exact potential function 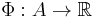\Phi: A \rightarrow \reals such that

\forall {a\in A} \; \forall {a_{i},b_{i}\in A_{i}} \; \Phi(b_{i},a_{-i})-\Phi(a_{i},a_{-i}) = u_{i}(b_{i},a_{-i})-u_{i}(a_{i},a_{-i})

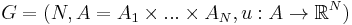A game G=(N,A=A_{1}\times...\times A_{N}, u: A \rightarrow \reals^N) is a general (ordinal) potential game if there is an ordinal potential function 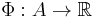\Phi: A \rightarrow \reals such that

\forall {a\in A} \forall {a_{i},b_{i}\in A_{i}}\; sign(\Phi(b_{i},a_{-i})-\Phi(a_{i},a_{-i})) = sign(u_{i}(b_{i},a_{-i})-u_{i}(a_{i},a_{-i}))

where sign denotes the Sign function.

A simple example

+1 –1
+1 +b1+w, +b2+w +b1–w, –b2–w
–1 –b1–w, +b2–w –b1+w, –b2+w
Fig. 1: Potential game example

In a 2-player, 2-strategy game with externalities, individual players' payoffs are given by the function ui(si, sj) = bi si + w si sj, where si is players i's strategy, sj is the opponent's strategy, and w is a positive externality from choosing the same strategy. The strategy choices are +1 and −1, as seen in the payoff matrix in Figure 1.

This game has a potential function P(s1, s2) = b1 s1 + b2 s2 + w s1 s2.

If player 1 moves from −1 to +1, the payoff difference is Δu1 = u1(+1, s2) – u1(–1, s2) = 2 b1 + 2 w s2.

The change in potential is ΔP = P(+1, s2) – P(–1, s2) = (b1 + b2 s2 + w s2) – (–b1 + b2 s2 – w s2) = 2 b1 + 2 w s2 = Δu1.

The solution for player 2 is equivalent. Using numerical values b1 = 2, b2 = −1, w = 3, this example transforms into a simple battle of the sexes, as shown in Figure 2. The game has two pure Nash equilibria, (+1, +1) and (−1, −1). These are also the local maxima of the potential function (Figure 3). The only stochastically stable equilibrium is (+1, +1), the global maximum of the potential function.

+1 –1
+1 5, 2 –1, –2
–1 –5, –4 1, 4
Fig. 2: Battle of the sexes (payoffs)
+1 –1
+1 4 0
–1 –6 2
Fig. 3: Battle of the sexes (potentials)

A 2-player, 2-strategy game is cannot be a potential game unless

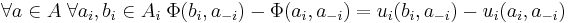
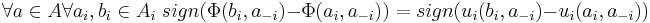
[u_{1}(%2B1,-1)%2Bu_1(-1,%2B1)]-[u_1(%2B1,%2B1)%2Bu_1(-1,-1)] = [u_{2}(%2B1,-1)%2Bu_2(-1,%2B1)]-[u_2(%2B1,%2B1)%2Bu_2(-1,-1)]

References

External links